
기초 원리
한 줄로 말하면 인공지능 모델에 데이터를 넣고 내가 원하는 답과의 차이를 줄이는 것이다.
그럼 모델은 어떻게 생겼고, 원하는 답은 무엇이고, 답과의 차이는 어떻게 구할까
모델
인공지능 모델의 직관은 "세상을 선(곱하기와 더하기)으로 표현하고 싶다."이다.
단순한 것으로 복잡한 것을 추측하는 이유는 그것을 계산할 식을 구하기 어렵기 때문이다.
내가 계산할 수 있는 것으로 식조차 모르는 것을 푸는 방법이다.
흔히 인공지능 모델 기초를 찾아보면
$$\mathbf{W}x + b$$
W(가중치), x(입력값), b(편향)로 표현한다.
흔히 알고 있는 일차함수이다. 어떻게 일차함수가 다른 것을 표현한다는 것일까?

무식하게 표현하여 이어 붙이기라 말할 수 있다. 검은색 선을 표현하기 위해 빨간색과 노란색 선을 이어 붙여 표현할 수 있다.


일차함수 여러 개를 사용해 왼쪽처럼 만들 수 있을 것 같다.
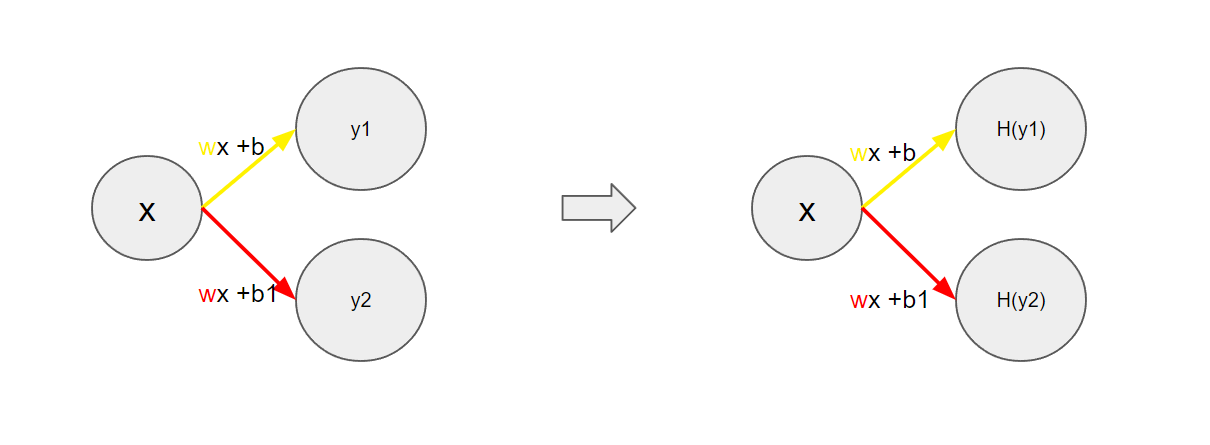
눈치챈 사람도 있겠지만, 단순히 일차함수만으로 곡선을 만들 수 없다.
y1과 y2에 어떤수를 곱하고 더해도 결국 wx+b로 곧 일차함수이다.
세로선을 기점으로 활성화되고 비활성화되는 선을 구부리는 역할로 비선형식을 곱해주어야 복잡한 것을 표현할 수 있다.
이 비선형식을 활성화함수(Activation Function)라 부르며 종류가 다양하게 있다.
가중치와 편향은 모델이 학습함에 따라 변하는 값이다. 이를 Parameter라고 부른다.
여기까지 정리하면 인공지능 모델은 일차함수로 구성되며 계수는 가중치, y절편은 편향으로 부른다.
복잡한 모양을 만들기 위해서는 비선형의 식을 곱해줘야 한다.
원하는 답이 무엇인가(Supervised Learning)
AND 게이트는 입력값 2개로 0 또는 1 값을 받아 둘 다 1이어야 1, 둘 중 하나라도 0이면 0인 것으로 우린 이미 답을 알고 있으므로 지도학습을 통해 진행할 것이다.

간단하게 하나의 퍼셉트론으로 예시를 보자
소문자 y는 모델의 결과값 대문자 Y는 실제 정답, x는 입력값이다.
$$ w_{1,1} =0.1 , w_{1,2} =-0.12, b=0 $$
으로 생겼다고 가정해보자

그럼 계산된 0.1의 값이 결과로 볼 수 있지만 우리는 아직 활성화 함수를 지나지 않았다. 여기서 활성화 함수의 역할은 이전 설명 같은 작용뿐만 아니라 값이 0과 1 사이로만 나오도록 하고 싶기 때문이다. sigmoid 함수를 사용할 것이다.
$$ \sigma = \frac{1}{1+e^{-y}} $$

답과 차이를 구하는 법 (Loss function)
모델이 답을 내놓았는데 실제 답과의 차이는 어떻게 구할 것인가? 단순히 빼기에 절댓값을 씌워 거리로 표현할 수도 있지만, 정답이 1일 때 결과가 0으로 갈수록 무한대에 가고 정답이 0일 때 결과가 1로 갈수록 무한대에 가도록 만들고 싶다.
그것을 수식으로 표현한 것이다.
$$ L = -Yln(y) - (1-Y)ln(1-y) $$
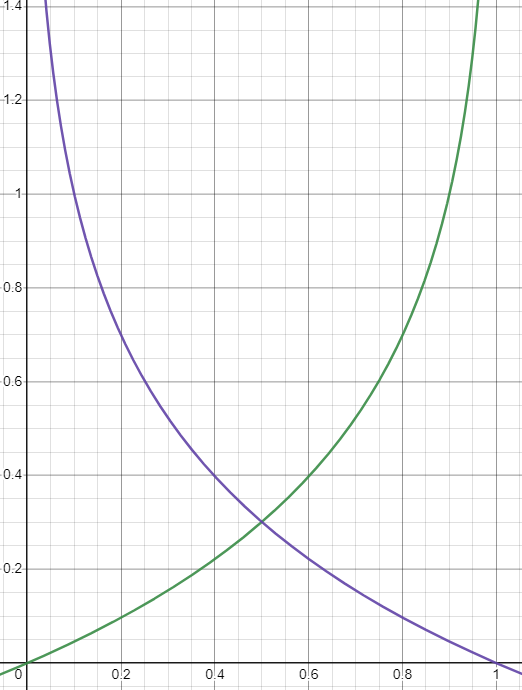
Y(정답)가 0이면 초록색 그래프가 되고, 1이면 보라색이 된다.
Binary Cross-Entropy라고 부른다.

답과의 차이 즉 Loss는 답과 멀수록 커지게 만들어야 하며 그 식을 Loss function이라고 부른다.
답과 차이를 줄이는 법 (Optimization)
그러면 어떻게 차이를 줄일 수 있을까.
시간이 무한이다 혹은 양자컴퓨터가 있다라면 모든 값을 대입해 가장낮을 Loss 값을 찾을 수도 있을 것이다.
이는 어두운 방안에 휴대폰 찾기 위해 방에 있는 모든 만질 수 있는 건 다 확인해 보는 것이다.
그럼 간단하게 우리가 할 수 있는 건 내 위치에서 더듬더듬 확인하듯 찾는 것이다.
경사하강법

더듬더듬하는 방법은 경사하강법이다.
위의 그림처럼 경사에 맞게 조금씩 움직이면 마치 물 흐르듯 점점 Loss값을 줄일 수 있을 것 같다.
하지만 저 그래프 모양을 모르거나 알기 어렵기 때문에 각 변수에 따라 얼마큼 영향을 주는 지만 파악하면 된다.
연쇄법칙(Chain-Rule)
$$ \frac{\partial L}{\partial w},\frac{\partial L}{\partial b} $$
우리가 궁금한 것은 변수인 W와 b가 얼마큼 Loss에 영향을 주는지 알아야 한다.
이에 연쇄법칙을 사용해 다음과 같이 구할 수 있다.
$$ \frac{\partial L}{\partial \sigma} = -\frac{-Y}{\sigma} + \frac{1-Y}{1-\sigma} $$
$$ \frac{\partial L}{\partial \sigma}* \frac{\partial \sigma}{\partial y} = \frac{\partial L}{\partial y}$$
$$ \frac{\partial L}{\partial y}* \frac{\partial y}{\partial w} = \frac{\partial L}{\partial w}$$
$$ \frac{\partial L}{\partial y}* \frac{\partial y}{\partial b} = \frac{\partial L}{\partial b}$$
시그마의 대한 Loss 변화를 통해 w와 b의 영향력을 파악할 수 있다.
다음은 직접 계산하는 과정이다.
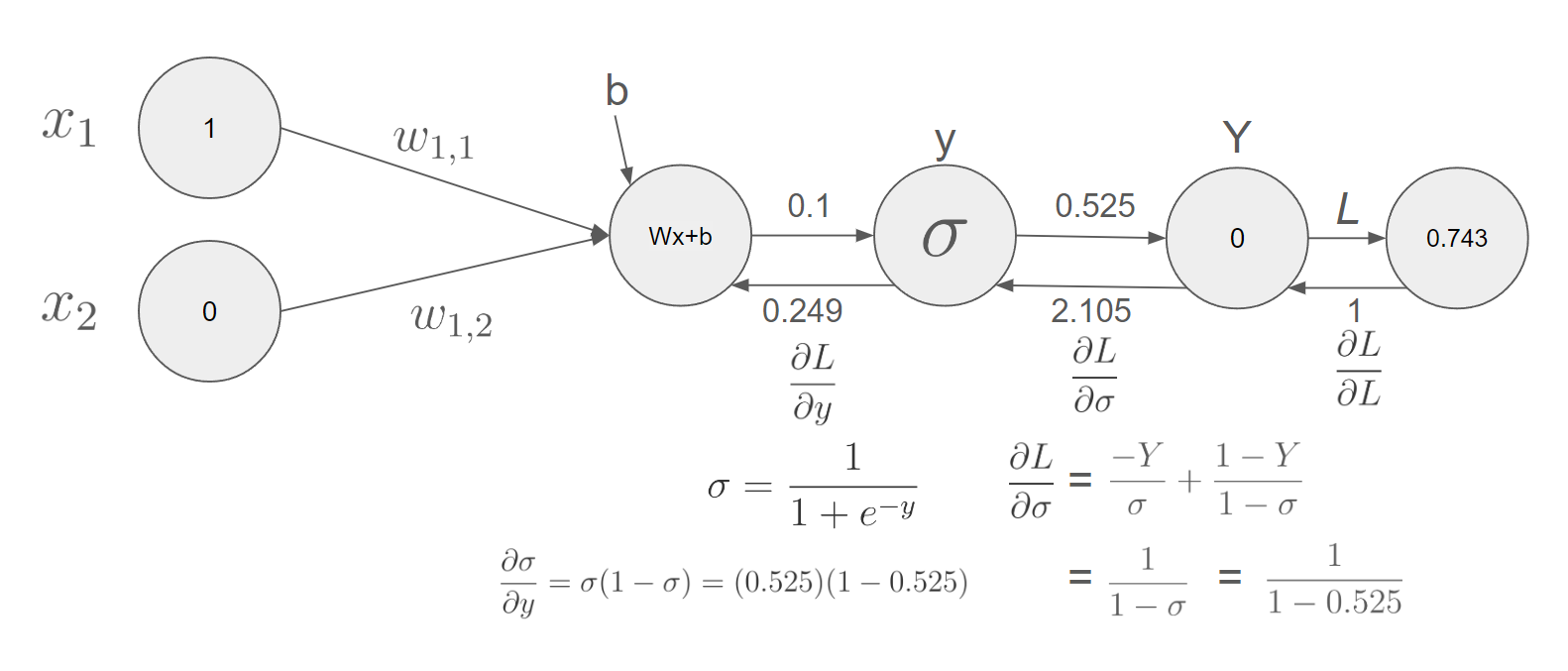
$$ \frac{\partial y}{\partial w_{1,1}} = \frac{\partial}{\partial w_{1,1}}(w_{1,1}*x_{1} + w_{1,2}*x_{2} +b) = x_1 $$
$$ \frac{\partial y}{\partial w_{1,2}} = \frac{\partial}{\partial w_{1,2}}(w_{1,1}*x_{1} + w_{1,2}*x_{2} +b) = x_2 $$
$$ \frac{\partial y}{\partial b} = \frac{\partial}{\partial b}(w_{1,1}*x_{1} + w_{1,2}*x_{2} +b) = 1 $$
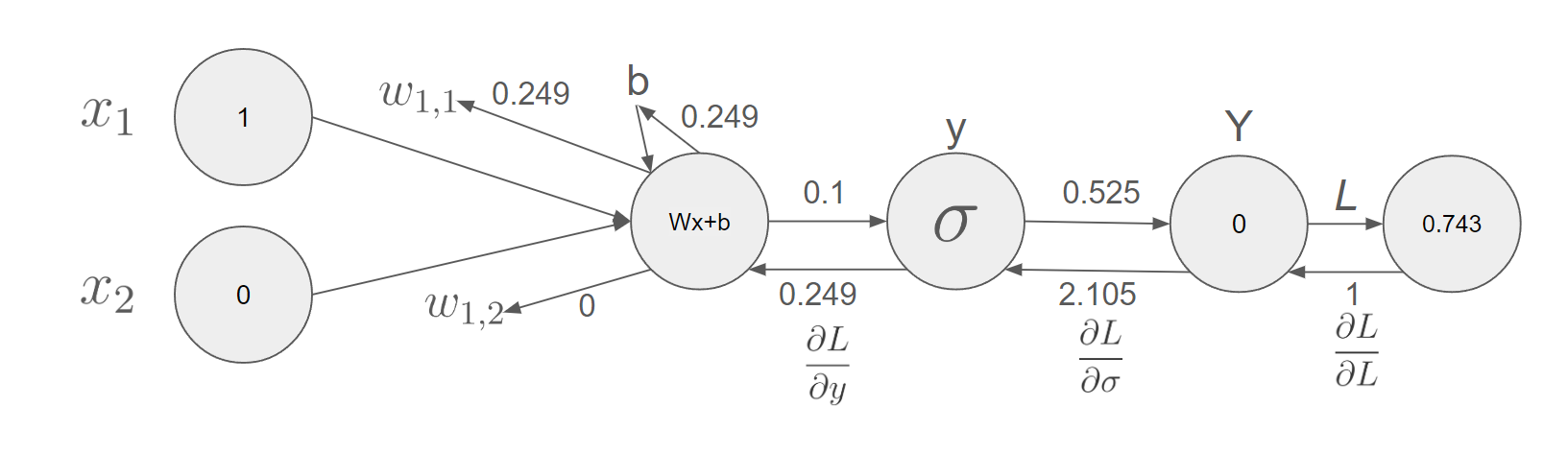
드디어 각 변수마다 Loss에 얼마큼 기울기를 가졌는지 알았다.
그러면 어떻게 변수를 업데이트할까?
가장 단순히 접근하면 딱 변화한 만큼에서 계수를 곱만큼 빼는 것이다.
이번에는 계수를 1이라 하겠다.
$$new\ w_{1,1} = w_{1,1} - lr * \frac{\partial L}{\partial w_{1,1}} = 0.1 - 1 * 0.249 $$
$$new\ w_{1,2} = w_{1,2} - lr * \frac{\partial L}{\partial w_{1,1}} = -0.12 - 1 * 0 $$
$$new\ b = b - lr * \frac{\partial L}{\partial b} = 0 - 1 * 0.249 $$
여기서 lr는 learning rate의 약자로 사람이 정해주는 값이다. 이를 하이퍼파라미터라 한다.
과연 이전보다 나아졌나 보자.
이전의 모델의 결과는 0.525이지만
업데이트 이후의 결과는
$$\frac{1}{1 + e^{-(-0.149 * 1 + -0.12 * 0 + (-0.249))}} = 0.402$$
조금 더 정답인 0에 근접했다.
이 과정을 반복하다 보면 최적의 파라미터를 찾아갈 수도 있다.

안녕하세요, 콰트로 로켓단 로이입니다.
나중에 자료가 부족해지지만 절대 귀찮아서 그런 거 아닙니다. 크흠
계산은 직접 해보시는 게 좋습니다.
이미 알고 있어야 이해할 수 있는 것을 직관적으로 작성하려다 보니 부족한 면이 있습니다.
조금 더 자세히 알고 싶은 분들을 위해 기초 자료들도 따로 작성해 보겠습니다.
'知 > job지식' 카테고리의 다른 글
| [Autocad] 외부참조(xref)가 연하게 보일때 (0) | 2024.06.28 |
|---|---|
| [Autocad] 외부참조(xref)-전체경로, 상대경로 차이 (0) | 2024.06.27 |
| [RL] Value functions (0) | 2024.05.31 |
| [RL] Markov Decision Process(MDP) (0) | 2024.05.30 |
| [Autocad] 외부참조 설정값이 원래대로 돌아갈 때 (0) | 2024.05.29 |